Functions, domain and range

Adapted from OpenStax College Algebra 2e¹

A function is a relation in which each possible input value leads to exactly one output value.

The input values make up the domain, and the output values make up the range.

We denote the domain and range of a function $f$ by $D_{f}$ and $R_{f}$ respectively.

Defining functions

We can define a function by giving its rule and describing its domain using the following notation:

$f : x \mapsto x^{2} + 1, for x \in ℝ, - 1 < x < 3 .$

The rule, or formula for the function $f$ is given by $f (x) = x^{2} + 1,$ allowing us to do computations such as $f (3) = 3^{2} + 1 = 10 .$

The domain of $f$ is given by $- 1 < x < 3 .$ Written in set notation, we have $D_{f} = (1,3) .$

Domain of a function

We should specify the domain when defining a function, as seen in the above example. The reason for this could be due to context. For example, if $x$ represents the number of hours in a day we study, then an appropriate domain would be $[0, 24] .$

Largest possible domains

The domain could also be due to considerations of what is mathematically permitted. For example, we cannot

divide by zero,
take square roots of negative numbers, or,
take the logarithm of zero or a negative number.

For example, the function

$f : x \mapsto \frac{1}{x - 2}, for x \in ℝ, x \neq 2$

has $x = 2$ omitted from its domain to avoid division by zero. Meanwhile, the largest possible domains for $g (x) = \sqrt{x + 3}$ is $D_{g} = [- 3, \infty)$ while that of $h (x) = \ln (x + 3)$ is $D_{h} = (- 3, \infty) .$

Range of a function

Using graphs to find the range

We recall that the range of a function refers to the set of all possible output values. A graph helps us find the range as we can visualize all the possible values of $y .$

As the following examples will illustrate, the important features of graphs that often affect the range of functions are:

end-points (be careful of inclusive vs exclusive cases!),
turning points,
asymptotes.

Examples

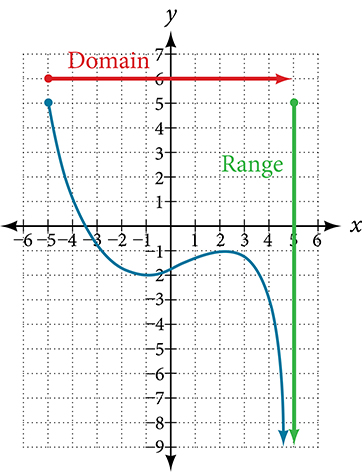
range of a function using end point

The above function has a left end point with coordinate $(- 5,5) .$ By considering all possible $y -values,$ we get the range $R_{f} = (- \infty, 5] .$

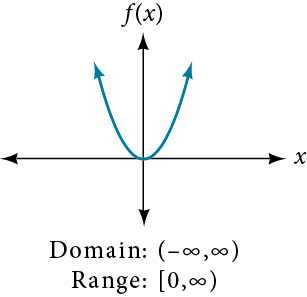
range of a function using turning point

The above function has both end points tending towards infinity. However, there is a minimum point on our graph at the origin, which appears in the computed range of $[0, \infty) .$

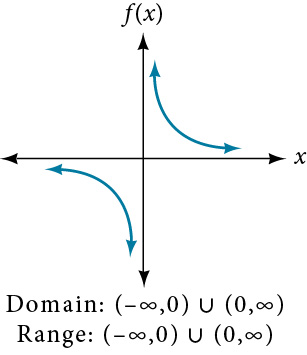
range of a function using asymptote

For this last example above, the range consists of all values except $0$ which is a result of the horizontal asymptote $y = 0 .$ Hence we can write the range as a union of two exclusive intervals.

Content in this page is adapted from OpenStax College Algebra 2e by Jay Abramson under the Creative Commons Attribution License.
Access for free at https://openstax.org/books/college-algebra-2e/pages/3-1-functions-and-function-notation ↩︎