Existence of inverse functions
Adapted from OpenStax Calculus Volume 11
Introduction to inverse functions
An inverse function reverses the operation done by a particular function. In other words, whatever a function does, the inverse function undoes it.
We denote the inverse of by
For example, if and we can make use of the function to find The inverse function aims to take the value and get back the original value of We can check that the function achieves this aim (we will learn how to find this in a later section).
Inverse functions may not exist
Consider the function It is a function: every input leads to exactly one output However, the reverse is not true: an output of could have come from either or In such a case we say that the inverse function does not exist.
One-to-one functions
The earlier function sends each input to a different output while will sometimes sends different inputs to the same output. This is what allows to have an inverse while does not.
We call this behavior of sending each input to a different output a one-to-one function.
We can check if a function is one-to-one (and thus its inverse exist) by employing the horizontal line test.
Horizontal line test
A function is one-to-one and has an inverse if and only if every horizontal line intersects the graph of no more than once.
The following two examples illustrate how to phrase the horizontal line test for the cases where is one-to-one and has an inverse, and where is not one-to-one and does not have an inverse.
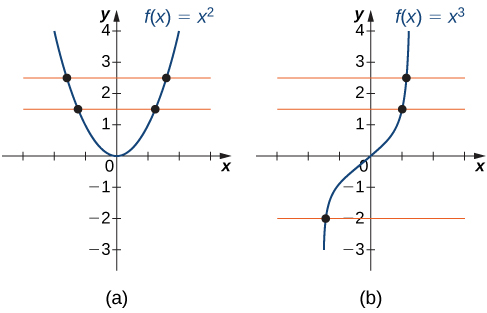
Inverse does not exist
The horizontal line intersects the graph of more than once. Thus, is not one-to-one and does not have an inverse.
Inverse exist
All horizontal lines intersects the graph of at most once. Thus, is one-to-one and has an inverse.
-
Content in this page is adapted from OpenStax Calculus Volume 1 by Gilbert Strang and Edwin “Jed” Herman under the Creative Commons Attribution Noncommercial Sharealike 4.0 License.
Access for free at https://openstax.org/books/calculus-volume-1/pages/1-4-inverse-functions↩︎