Relationship between a function and its inverse

Adapted from OpenStax Calculus Volume 1¹

Consider the graph of f shown below and a point $(a, b)$ on the graph.

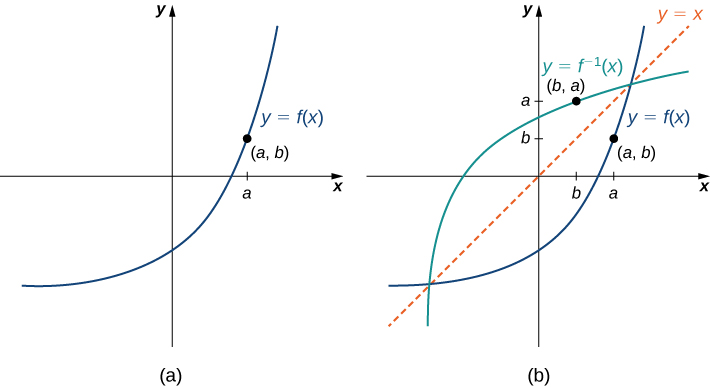
relationship between a function and its inverse

Since $b = f (a),$ then $f^{- 1} (b) = a .$ Therefore, when we graph $f^{- 1},$ the point $(b, a)$ is on the graph.

Symmetry of the graphs

As a result, the graph of $f^{- 1}$ is a reflection of the graph of $f$ about the line $y = x .$ In other words, the graphs of $y = f (x)$ and $y = f^{- 1} (x)$ are symmetrical about the line $y = x .$

Using the relationship

In a previous example, we have found that the inverse of $f (x) = x^{2} + 4 x$ for $x \leq - 1$ is $f^{- 1} = - 2 - \sqrt{x + 4} .$

If we want to find the intersection between the graphs of $y = f (x)$ and $y = f^{- 1} (x),$ we can equate the two to get the equation

$x^{2} + 4 x = - 2 - \sqrt{x + 4}$

Solving this could be quite challenging. Using the symmetrical relationship between the graphs, we can find the answer in a simpler manner (in fact, we don’t even need to find the formula for $f^{- 1}$ ). We illustrate this using the following example:

Question:
The function $f$ is given by

$f : x \mapsto x^{2} + 4 x, x \in ℝ, x \leq - 2,$

Find the $x$ -coordinate of the point of intersection between the graphs of $y = f (x)$ and $y = f^{- 1} (x) .$

Solution:

Since the graph of $y = f^{- 1} (x)$ is a reflection of the graph of $y = f (x)$ about the line $y = x,$ we can solve for the intersection between the two graphs by finding the intersection of $y = f (x)$ with the line $y = x .$

$\begin{matrix} x^{2} + 4 x = x \\ x^{2} + 3 x = 0 \\ x (x + 3) = 0 \\ x = 0 or x = - 3 \end{matrix}$

Since $x \leq - 2,$ we have our answer $x = - 3 . ∎$

Content in this page is adapted from OpenStax Calculus Volume 1 by Gilbert Strang and Edwin “Jed” Herman under the Creative Commons Attribution Noncommercial Sharealike 4.0 License.
Access for free at https://openstax.org/books/calculus-volume-1/pages/1-4-inverse-functions ↩︎