Hyperbolas

Adapted from OpenStax College Algebra 2e¹

Equations of hyperbolas

Horizontal and vertical hyperbolas have the following equations in standard form

$\begin{aligned} Horizontal hyperbola: & \frac{(x - h)^{2}}{a^{2}} - \frac{(y - k)^{2}}{b^{2}} = 1 \\ Vertical hyperbola: & \frac{(y - k)^{2}}{b^{2}} - \frac{(x - h)^{2}}{a^{2}} = 1 \end{aligned}$

Key features of hyperbolas

features of hyperbolas

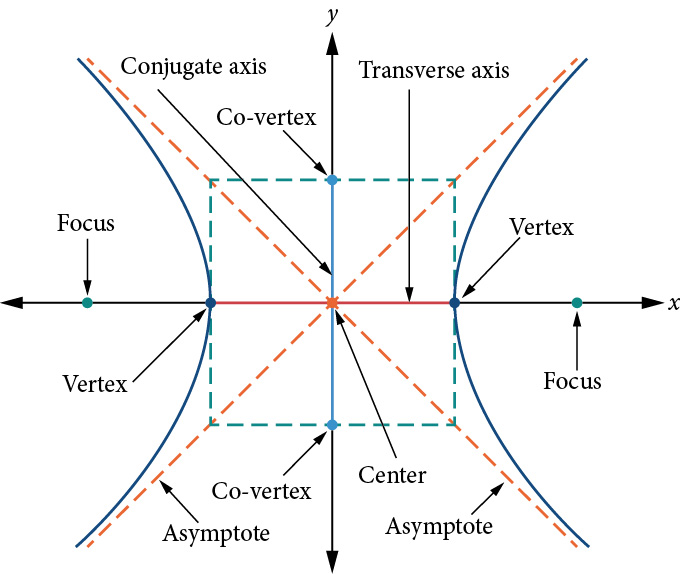
The diagram above shows the key features of hyperbolas. In particular, the following features are most useful in drawing hyperbolas:

center
vertices
asymptotes

Drawing a hyperbola

Center

Just like in drawing an ellipse, we draw a hyperbola by first identifying its center. For an equation of standard form above, the center has coordinates $(h, k) .$

Horizontal vs vertical hyperbolas

We then deduce whether our hyperbola is horizontal or vertical, based on its equation (does $x$ or $y$ appear first in the difference in our equation?).

Vertices

We then locate the vertices. For a horizontal hyperbola, the two vertices are $a$ units on the left and right of the center, with coordinates $(h - a, k)$ and $(h + a, k) .$

For a vertical hyperbola, the two vertices are $b$ units above and below the center, with coordinates $(h, k - b)$ and $(h, k + b) .$

Asymptotes

For both horizontal and vertical hyperbolas, there are two oblique asymptotes that pass through the center. They have gradient $\pm \frac{b}{a}$ so their equations are

$y - k = \frac{b}{a} (x + h)$
$y - k = - \frac{b}{a} (x + h)$

With these features set up on our graph, we can then proceed to draw our hyperbolas. We start off at one corner of an asymptote, bend towards and pass through the vertex and then go back towards the other asymptote.

We draw to the left and right of the center for,horizontal hyperbolas. For vertical hyperbolas, we draw above and below the center.

Example 1

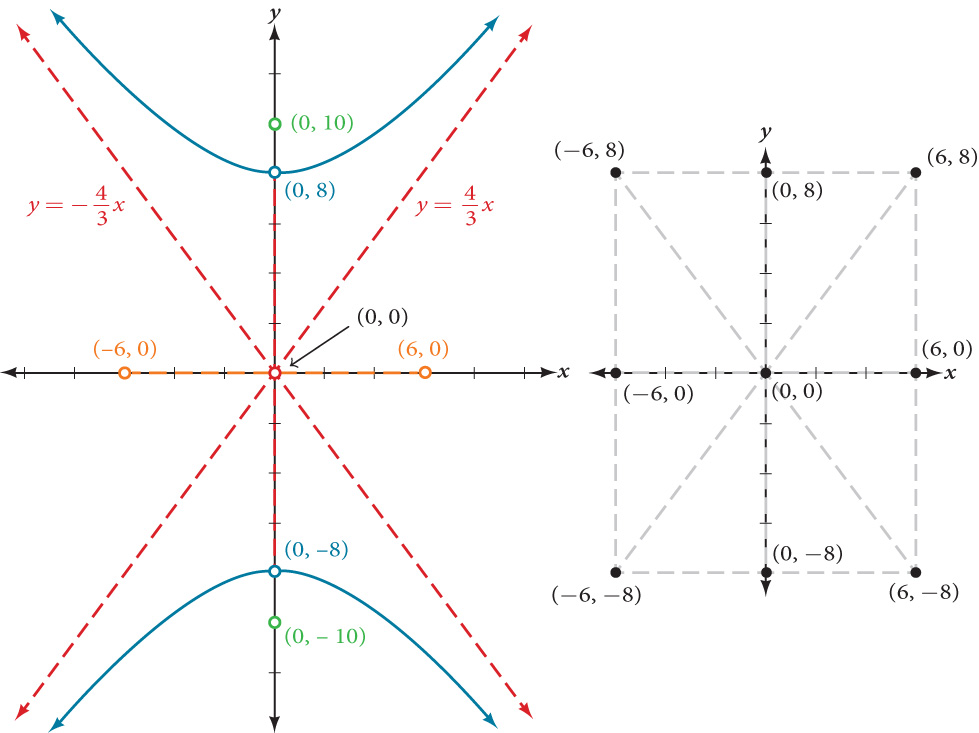
The following is a sketch of the vertical hyperbola with equation

$\frac{y^{2}}{64} - \frac{x^{2}}{36} = 1$

The origin is the center of the hyperbola, with vertices $(0, 8)$ and $(0, - 8) .$

The gradient of the asymptotes are $\pm \frac{8}{6} = \pm \frac{4}{3}$ so the equations of the asymptotes are $y = \pm \frac{4}{3} x .$

vertical hyperbola

Example 2

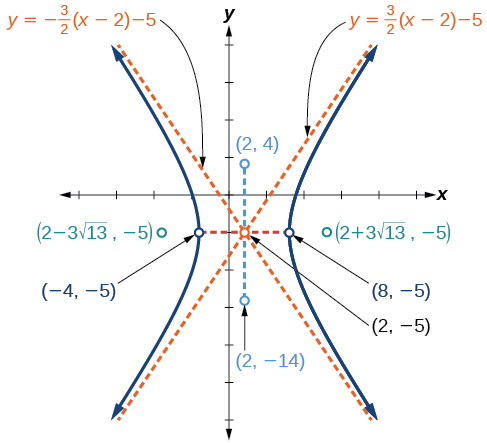
The following is a sketch of the horizontal hyperbola with equation

$\frac{(x - 2)^{2}}{36} + \frac{(y + 5)^{2}}{81} = 1$

The center of the hyperbola is $(2, - 5),$ and it has vertices $6$ units horizontally from the center so their coordinates are $(- 4, - 5)$ and $(8, 5) .$

The gradient of the asymptotes are $\pm \frac{9}{6} = \pm \frac{3}{2}$ so the equations of the asymptotes are $y + 5 = \pm \frac{3}{2} (x - 2) .$

horizontal hyperbola

Content in this page is adapted from OpenStax College Algebra 2e by Jay Abramson under the Creative Commons Attribution License.
Access for free at https://openstax.org/books/college-algebra-2e/pages/5-6-rational-functions ↩︎