Conic sections

Brief historical overview

Around 300 BCE, the Greek mathematician Menaechmus discovered shapes by intersecting a plane with right circular cones. He was able to obtain ellipses, hyperbolas and parabolas depending on how he tilted the plane.

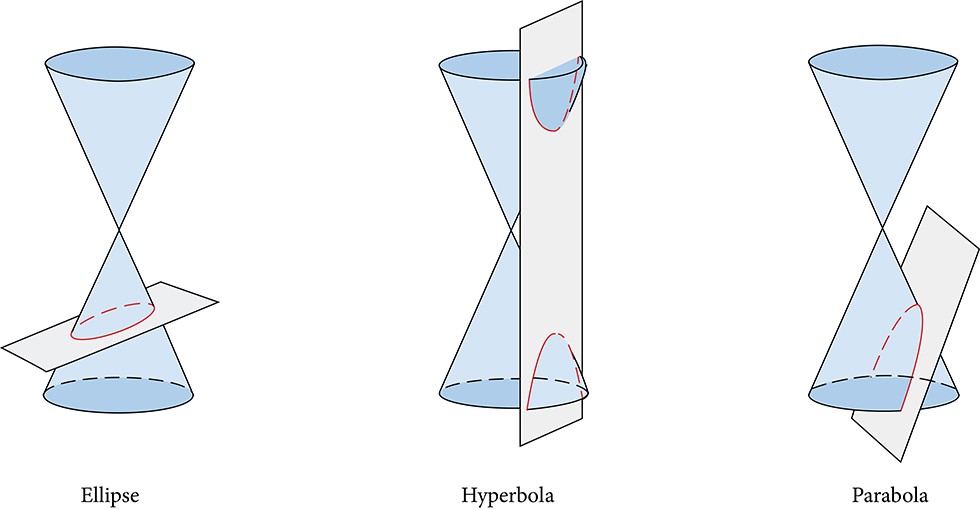
Around 2000 years later, we see these shapes in real life applications. The ellipse describes how planets orbit around the sun, while the hyperbola describes magnetic repulsion.

Standard forms

We describe these shapes algebraically by the following equations:

$$\begin{array}{rlrl}& \text{Ellipse:}& & \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\\ & \text{Hyperbola:}& & \frac{x^2}{a^2}-\frac{y^2}{b^2}=1\\ & \text{Hyperbola:}& & \frac{y^2}{a^2}-\frac{x^2}{b^2}=1\\ & \text{Parabola:}& & y=a{x}^2\\ & \text{Parabola:}& & x=a{y}^2\end{array}$$

The ellipses and hyperbolas have center at the origin $(0,0)$ while the parabolas have vertex at the origin. We will explore more about these features in the subsequent sections.

When the center or vertex is not at the origin, the curves have equations:

$$\begin{array}{rlrl}& \text{Ellipse:}& & \frac{(x-h{)}^2}{a^2}+\frac{(y-k{)}^2}{b^2}=1\\ & \text{Hyperbola:}& & \frac{(x-h{)}^2}{a^2}-\frac{(y-k{)}^2}{b^2}=1\\ & \text{Hyperbola:}& & \frac{(y-k{)}^2}{a^2}-\frac{(x-h{)}^2}{b^2}=1\\ & \text{Parabola:}& & y=a(x-h{)}^2+k\\ & \text{Parabola:}& & x=a(y-k{)}^2+h\end{array}$$

We call these equations the standard form of each shape.

Completing the square

If a conics equation is not of standard form, we can convert to standard form by completing the square.

The following is an example where we convert the equation

$$x^2+6x+4y^2+5=0$$

into the standard form of an ellipse:

$$\begin{array}{c}{x}^2+6x+4y^2+5=0\\ (x+3{)}^2-9+4y^2+5=0\\ (x+3{)}^2+4y^2=4\\ \frac{(x+3{)}^2}{2^2}+\frac{y^2}{1^2}=1\end{array}$$