Extended curve sketching

Adapted from OpenStax College Algebra 2e¹

The techniques we have discussed to graph more complicated functions. The knowledge of the asymptotes and use of a graphing calculator will help us better understand the key features of the graphs.

Example 1

$Example : y = \frac{3 x^{2} + 2}{x^{2} + 4 x - 5}$

Long division

We can perform long division to express the equation of the curve as

$y = 3 + \frac{- 10 x + 17}{x^{2} + 4 x - 5}$

As $\frac{- 10 x + 17}{x^{2} + 4 x - 5}$ is a proper rational function, it will approach $0$ as $x \to \infty .$ Hence our curve has a horizontal asymptote $y = 3 .$

Factorizing the denominator

We can then factorize the denominator to get

$y = 3 + \frac{- 10 x + 17}{(x + 5) (x - 1)}$

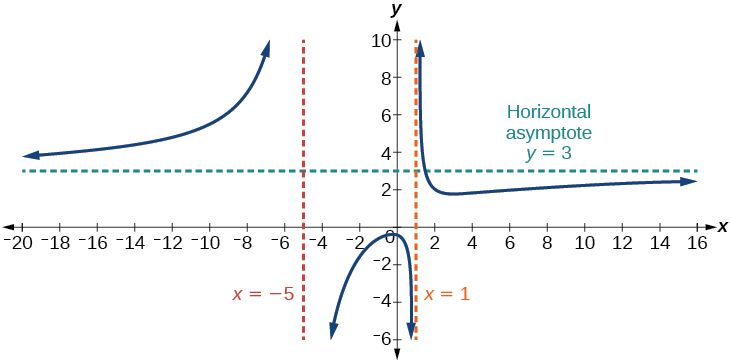
Hence the curve has vertical asymptotes $x = - 5$ and $x = 1 .$

Graph of example 1

y=(3x2+2)/(x2+4x-5)

Example 2

$Example : y = \frac{3}{2 e^{- x} + 1}$

This curve has no vertical asymptotes as the denominator $2 e^{- x} + 1$ is always positive.

Horizontal asymptotes

As $x \to - \infty,$ $e^{- x} \to \infty$ so $\frac{3}{2 e^{- x} + 1} \to 0 .$

As $x \to \infty,$ $e^{- x} \to 0$ so $\frac{3}{2 e^{- x} + 1} \to 3 .$

Hence our curve has two horizontal asymptotes $y = 0$ and $y = 3 .$

Graph of example 2

$y=3/(2e^{-x}+1)$

Content in this page is adapted from OpenStax College Algebra 2e by Jay Abramson under the Creative Commons Attribution License.
Access for free at https://openstax.org/books/college-algebra-2e/pages/5-6-rational-functions ↩︎