Oblique asymptotes

Adapted from OpenStax College Algebra 2e¹

In addition to horizontal and vertical asymptotes, we can also have oblique (slanted) asymptotes.

Asymptotes

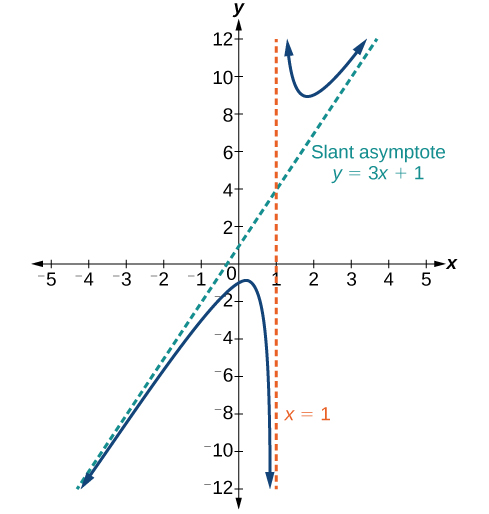
The curve of $y = a x + b + \frac{c}{d x + e}$ has a vertical asymptote $x = - \frac{e}{d}$ and an oblique asymptote $y = a x + b .$

Example

The curve of $y = 3 x + 1 + \frac{2}{x - 1}$ has a vertical asymptote $x = 1$ and an oblique asymptote $y = 3 x + 1 .$

oblique asymptote y=3x+1 + 2/(x-1)

Long division

Similar to the previous section, we can use long division to find asymptotes (including oblique ones) of improper rational functions.

For example, $\frac{3 x^{2} - 2 x + 1}{x - 2}$ can be rewritten as $3 x + 1 + \frac{2}{x - 1}$ via long division. We can now use this form to deduce that the asymptotes are $x = 1$ and $y = 3 x + 1 .$

Content in this page is adapted from OpenStax College Algebra 2e by Jay Abramson under the Creative Commons Attribution License.
Access for free at https://openstax.org/books/college-algebra-2e/pages/5-6-rational-functions ↩︎