Asymptotes

Adapted from OpenStax College Algebra 2e¹

Limits

Let us consider the function $f (x) = \frac{1}{x - 2} .$

While the function is undefined for $x = 2,$ we can use values of $x$ close to $2$ ( $2.1,$ $2.01,$ $2.001,$ etc). As we do that, the absolute value of $f (x)$ increases without bound (that is, to infinity).

Meanwhile, when $x$ gets larger and larger, $f (x) = \frac{1}{x - 2}$ gets smaller and smaller and approaches zero (even though it never actually achieves that value).

Arrow notation

To describe the above behavior, we can use the arrow notation:

$\begin{aligned} As x \to 2^{+}, & f (x) & \to \infty, \\ As x \to 2^{-}, & f (x) & \to - \infty, \\ As x \to \infty, & f (x) & \to 0 . \\ As x \to - \infty, & f (x) & \to 0, \end{aligned}$

As $x$ approaches $2$ from the right, $f (x)$ tends to infinity
As $x$ approaches $2$ from the left, $f (x)$ tends to negative infinity
As $x$ tends to infinity, $f (x)$ tends to zero
As $x$ tends to negative infinity, $f (x)$ tends to zero

Limit notation

We can also use the limit notation:

$\begin{aligned} \lim_{x \to 2^{+}} f (x) & = \infty, \\ \lim_{x \to 2^{-}} f (x) & = - \infty, \\ \lim_{x \to \infty} f (x) & = 0, \\ \lim_{x \to - \infty} f (x) & = 0 . \end{aligned}$

The limit of $f (x)$ as $x$ approaches $2$ from the right is infinity
The limit of $f (x)$ as $x$ tends to infinity is zero

Vertical and horizontal asymptotes

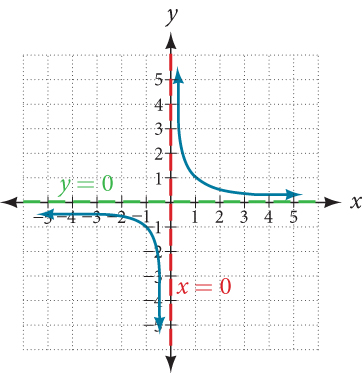
The asymptotes of a graph capture the infinite behavior of a function discussed above. Hence the graph of $y = \frac{1}{x - 2}$ has a vertical asymptote $x = 2,$ and a horizontal asymptote $y = 0 .$

The figure below shows the graph of $y = \frac{1}{x}$ with asymptotes $x = 0$ and $y = 0 .$

vertical and horizontal asymptotes of y=1/x

Exponential graphs

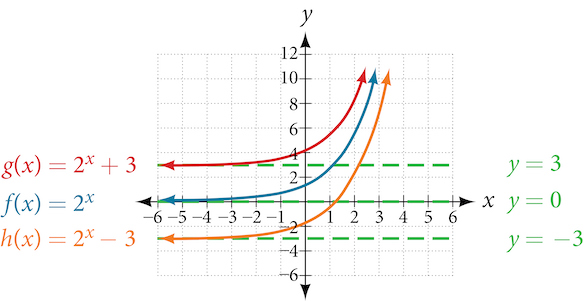
As $x \to - \infty,$ $e^{x} \to 0 .$ Hence exponential graphs have a horizontal asymptote. Our example $y = e^{x}$ has a horizontal asymptote $y = 0 .$

The figure below shows the horizontal asymptotes of other exponential graphs.

horizontal asymptotes of exponential graphs

Logarithmic graphs

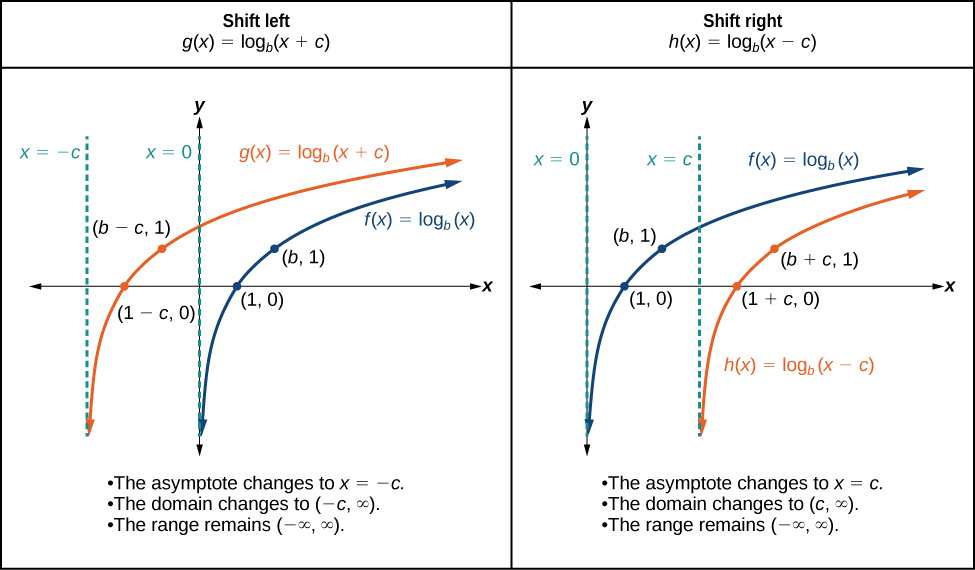
As $x \to 0^{-},$ $\ln x \to - \infty .$ Hence logarithmic graphs have a vertical asymptote. Our example $y = \ln x$ has a vertical asymptote $x = 0 .$

The figure below shows the vertical asymptotes of other logarithmic graphs.

vertical asymptotes of logarithmic graphs

Content in this page is adapted from OpenStax College Algebra 2e by Jay Abramson under the Creative Commons Attribution License.
Access for free at https://openstax.org/books/college-algebra-2e/pages/5-6-rational-functions ↩︎